Nutzt der Fahrgast im Fall konstanter Takte die Information aus, wie lange er schon an der Haltestelle wartet, so ist er in der Lage, seine erwarteten Restkosten gegenüber den bisher vorgestellten Modellen zu reduzieren. Beispielsweise weiß der Fahrgast nach einer Wartezeit von acht Minuten, dass eine Linie mit 10-Minuten-Takt innerhalb der nächsten zwei Minuten eintreffen muss. Er kann diese Information nutzen, um eventuell zuvor eintreffende, aber um mindestens zwei Minuten langsamere Linien zu ignorieren.
Diese Information hat der Fahrgast ganz unabhängig von der äußeren Infrastruktur. Sie zu unterstellen ist somit keine starke Annahme.
In diesem Fall hängt die optimale Linienmenge L* von der verstrichenen Wartezeit ab, ist also nicht mehr konstant. Die Ermittlung dieser Menge ist schwieriger als in den vorangegangenen Fällen. Es lässt sich nachweisen, dass L* folgende Gestalt hat.
Es gibt ein i* ≤ n und eine geordnete Folge von Zeitpunkten 0 ≤ ti* ≤ ... ≤tl, sodass im Zeitintervall Ij= (tj+1,tj] gerade Lj = {1, ..., j} die optimale Linienmenge bildet. tj ist dabei genau der Zeitpunkt t, ab dem die Rest-Reisezeit von Linie j größer oder gleich den erwarteten Restkosten (inklusive Wartezeit nach t) der Linien Lj-1 ist. Anders formuliert, ist tj die eindeutige Lösung für t in 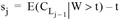 .
.
Die optimale Strategie ist die folgende. Falls der Fahrgast nach Wartezeit τ ∈ Ij eine Ankunft einer Linie aus Lj beobachtet, so steigt er in diese Linie ein. Andere Linien ignoriert er.
Man kann zeigen, dass diese Strategie die erwarteten Restkosten minimiert. Wie im Folgenden erläutert wird, entspricht sie dem realen Verhalten von Fahrgästen mehr, als ihre abstrakte Definition vermuten lässt.
Da der Fahrgast die Takte aller Linien kennt, erhöht sich mit fortgeschrittener Wartezeit sein Wissen darüber, welche der verfügbaren Linien sich noch lohnen. Auch vergleichsweise langsame Linien können zu Beginn der Wartezeit noch sinnvolle Alternativen darstellen. Es gibt jedoch einen Zeitpunkt, an dem die Bewertung „kippt”. Irgendwann ist der Erwartungswert für die verbleibende Wartezeit auf die schnelleren j-1 Linien geringer als die Differenz zwischen deren erwarteter Rest-Reisezeit und der Rest-Reisezeit von Linie j. Genau ab diesem Zeitpunkt lohnt es sich nicht mehr, Linie j zu benutzen – selbst wenn sie unmittelbar eintrifft. Die oben genannten Zeitpunkte tj sind genau die Momente, wo eine Linie j aus diesem Grund aus der optimalen Linienmenge L* herausfällt.
Beispiel
Betrachten wir folgende einfache Situation von zwei Linien.
|
Linie |
Fahrzeit |
Takt |
|
1 |
10‘ |
15‘ |
|
2 |
13‘ |
15‘ |
Der Fahrgast wartet maximal 15 Minuten auf die Weiterfahrt. Nach t Minuten beträgt die erwartete Rest-Reisezeit für Linie 1 noch genau 10 + (15 - t) / 2 Minuten. Um den Zeitpunkt zu ermitteln, ab dem dieser Erwartungswert geringer ist als die Fahrzeit von Linie 2, löst man 10 + (15 - t) / 2 ≤ 13 nach t auf und erhält t ≥9, setzt also t2 = 9.
Mit anderen Worten kann nach 9 Minuten ein Fahrzeug von Linie 2 ignoriert werden, da die um drei Minuten längere Reisezeit von Linie 2 durch die mittlere verbleibende Wartezeit auf Linie 1 nicht mehr wettgemacht wird.

